Machine Learning Part3

Machine Learning part 3: Chiziqli regressiya.

ML darslarimizning 3-qismiga keldik. Bugun men sizlarga chiziqli regressiya haqida gapirmoqchiman. Bu eng ko’p foydalaniladigan va tushunishga oson algoritmlardan biri hisoblanadi. Bu darsda o’rganish jarayoni qanday bo’layotganini chuqurroq ko’rib chiqamiz. Bunda sizga algebra kursidagi bilimlaringiz asqotadi. Lekin unchalik ko’p havotirga tushmang bu siz o’ylaganchalik murakkab narsa emas. Oldin aytganimdek, bizda o’rganiladigan malumotlar bazasi mavjud yani atribut va labellardan tashkil topgan. Atributlar obektlarni farqlash uchun ishlatiladigan belgilar to’plami.

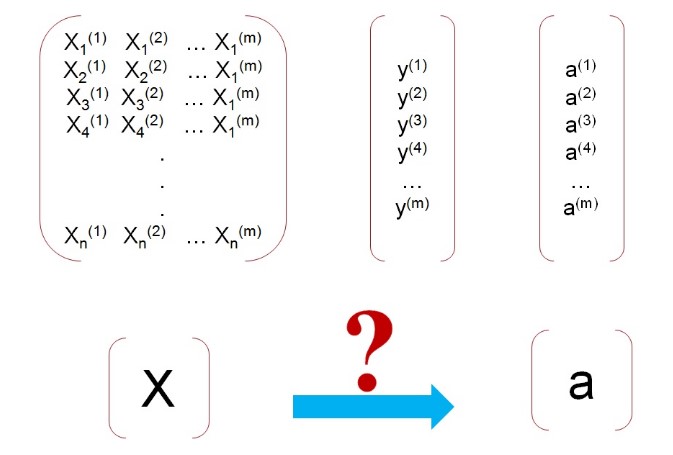
Buni esladingizmi? (birnchi mavzudan). X- atributlar va y- labellar. Demak o’rganiladigan malumotlar bazasini to’plaganimizdan keyin , uni kompyuter tomonidan o’rgnamiz(yani kompyuter o’rganib chiqadi bu bazani) Bu amaliyotdan keyin kompyuterga oldin umuman ko’rmagan atributlar to’plamini beramiz (yani X larni y larsiz). Kompyuter berilgan atributalar, X lar orqali obekt nomlarini aytadi ( yani bashorat qiladi). Bu bashoratni biz activation yoki a deb nomlaymiz.

Yuqoridagi rasamni ko’rganimizda miyyamizga kelgan birinchi savol kompyuter qanday qilib o’rganish jarayonida X lar orqali y ni topadi va qanday qilib berilgan X lar orqali a ni yani bashorat qiladi? Bu savollarga javob: o’rganuvchi algoritm orqali. Bu algoritm ishlashi uchun bizga aktivatsiya funksiyasi kerak bo’ladi.

Birinchi mavzuni tugatgan joyimizga yetib keldik. Aktivatsiya funksiyasi bu ML da eng muhim tushunchalardan bo’lib , bu tushuncha faqat chiziqli regressiya yoki mantiqiy regressiya kabi algoritimlarda emas balki bundan ham murakkab algoritmlarda qo’llaniladi. Aktivatsiya funksiyasi o’zi nima? Bu funksiya shunday funksiyaki berilgan X lar orqali a aktivatsiyalarni hisoblash uchun ishlatiladi.
Chiziqli regressiyada esa aktivizatsiya funksiyasi juda oddiy:

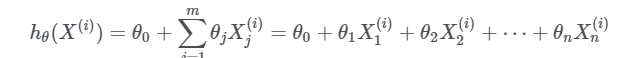
Yuqoridagi tenglikni tushuntirishga harakat qilaman. Birinchi, X da yuqoridagi va pastdagi ko’rsatkichlar nimani anglatadi? Tasavur qilamiz bizda o’rganiluvchi malumotlar bazasida 10 ta misol va har bir misolda 4 tadan atribut mavjud, bundan yuqori ko’rsatkichdagi i lar misollar tartibi va j lar misollarga tegishli atributlar tartibini ko’rsatar ekan. Yanada tushunarliroq bo’lishi uchun 10 ta misolni 1 ta atributga ega deb qaraymiz va quyidagicha aktivatsiya funksiyasiga ega bo’lamiz:

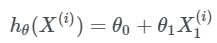
Bu huddi o’rta maktabda o’tilgan chiziqli funksiya o’xshab qoldi, to’g’rimi? Agar biz bu funksiya grafigini chizsak chiziqli grafikka ega bo’lamiz, chiziqli regressiya g’oyasi ham shundan iborat. Tassavur qilamiz bizning o’rganuvchi malumotar bazasi quyidagilardan tashkil topgan:

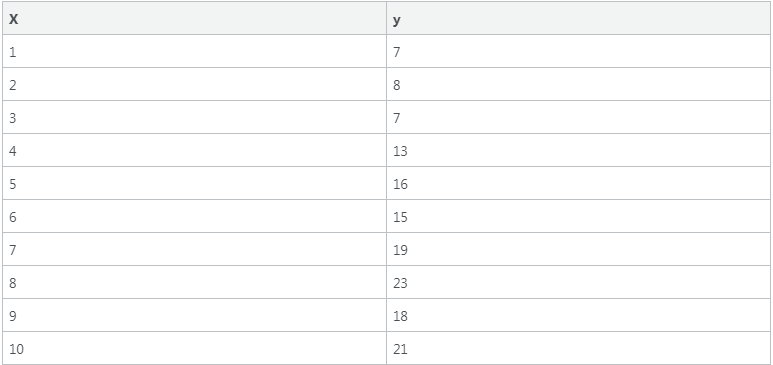
Agar buni koordinatalar o’qida tasvirlasak quydagiga ega bo’lamiz:

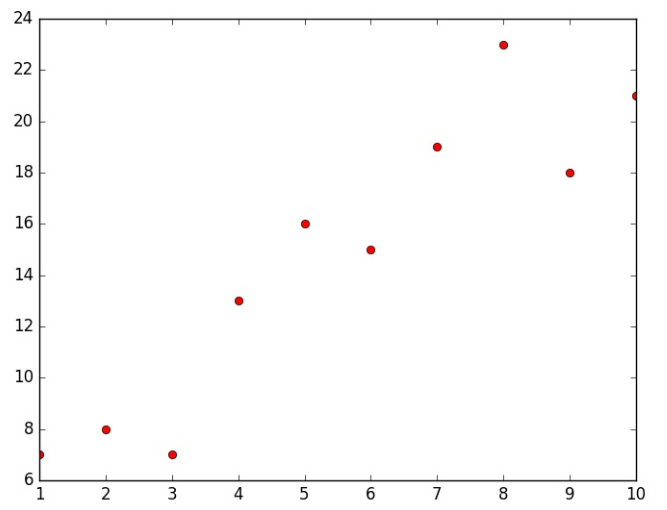
Demak, bizning vazifa shundan iborat bo’ladiki, shu nuqtalarni qanoatlantiruvchi funksiya topishimiz kerak. Chiziqli regressiyada bitta o’zgaruvchi bilan, chunki bizning aktivizatsiyali funksiyamiz to’g’ri chiziqdan iborat. Biz shunday chiziq topishimiz kerakki , bu chiziq shu nuqtalarning deyarli hammasidan o’tishi kerak. Lekin, qanday boshlaymiz? Biz tasodifiy parametrlardan foydalanib hisoblashni boshlaymiz,yani w,b larni tasadifiy tanlaymiz. Keling ikkalisini ham 1 deb hisoblaymiz. Endi biz aktivizatsiya funksiyasini hisoblashimiz mumkin: a=1+x. Endi bu funksiya grafigini chizadigan bo’lsak quyidagiga ega bo’lamiz:

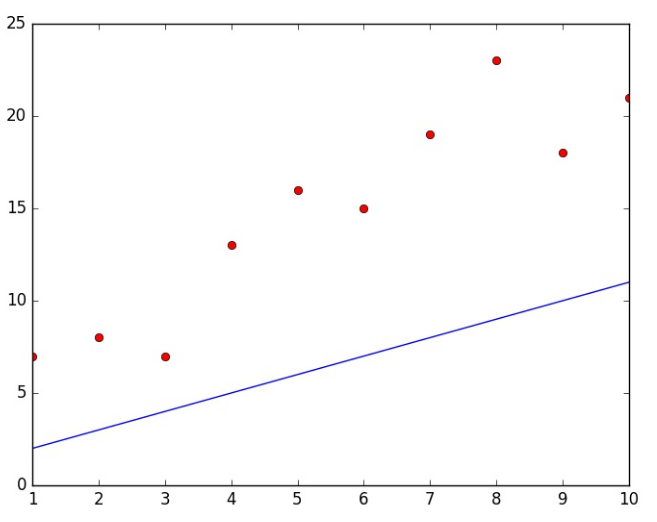
Ko’rinib turibdiki aktivizatsiya funksiyasining grafigi bizning malumotlar bazamizdagi bironta nuqtani kesib o’tmadi. Lekin bu hali yomon degani emas, chunki biz parametrlarni tasodifiy ravishda tanladik va hech qanday o’rganish boshlangani yo’q hali. Endi quyudagi savol paydo bo’ladi qanday qilib aktivizatsiya funksiyasini o’zgartirsak, u shu nuqtalarning deyarli barchasidan o’tadi? Boshqacharoq qilib aytadigan bo’lsak kompyuterni aktivizatsiya funksiyasini to’g’ri tanlashga qanday o’rgatishimiz mumkin? Eng birinchi qilishimiz kerak bo’lgan narsa bu hozirgi aktivizatsiya funksiyamizni baholash bo’ladi. Buni hisoblash yo’llaridan biri Funksiya qiymati(cost function). Funksiya qiymati labellardan bashorotlarni ayirish orqali bajariladi (yani to’g’ri javobdan kompyuter bergan javobni ayirish orqali amalga oshiriladi). Funksiya qiymatini hisoblash usullaridan biri “xatolikning o’rtacha kvadratik funksiyasi” hisoblanadi qaysiki chiziqli regressiyada eng mos keladigan va mashinali o’rganishni endi boshlaganlar uchun tushunarliroq bo’lgani. Xatolikning o’rtacha kvadratik funksiyasi. Birinchidan bu funksiya qanday ko’rinishga ega degan savolga javob topamiz:

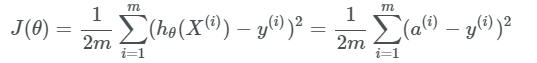
Endi hamma narsa tushunarliroq bo’lib qoldi. Bu funksiya xatoliklar kvadratining o’rtacha qiymatini hisoblaydi. Yani bashorotlar hθ(X(i)) va labellar y(i) orasidagi farqning kavadratlarini o’rtacha qiymatini. Yuqoridagi tenglikdan ko’rinib turibdiki J(θ) qancha katta bo'lsa demak funksiyamiz shunchalik yomon. Aksincha J(θ) qiymat qanchalik nolga yaqin bo'lsa aktivizatsiya funksiyamiz shunchalik yaxshi, yani bashorotlar va labellar bir biriga juda yaqin ekanligini anglatadi. Shu yerda yana bir savol tug’ilishi mumkin nimaga aynan ayirmalarning kavadratlarini hisoblayapmiz , nimaga shunchaki ayirmalarning o’zini hisoblamaymiz? Kabi. Bunga javob siz shunday qilishingiz mumkin lekin ayirmalarning kavadratlarini hisoblash ancha effektivroq ekanligi tajribalarda malum bo’lgan. Endi yana bir yangi tushuncha gradient tushush (gradient descent) bilan tanishamiz.

Gradient tushush. Chuqurroq kirishdan oldin xatolikning o’rtacha kvadratik funksiyasiga qaytsak.

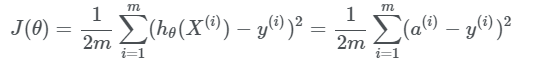
Bu yerda  θ parametr funksiya qimatining o'zgaruvchisi hisoblanadi. Soddalahstirish uchun  θ ni faqat θ1 dan tashkil topgan deb hisoblasak. U holda funksiya qiymati quydagiga ega bo’lamiz:

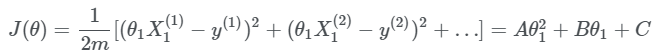
Bundan ko’rinib turibdiki biz kvadrat funksiyaga ega bo’ldik, agar bu funksiya grafigini chizadigan bo’lsak quyidagini olamiz:

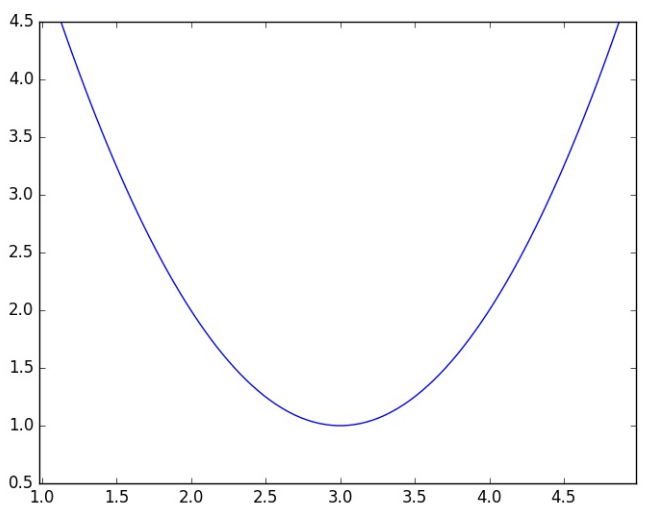
Yuz marta eshitgandan bir marta ko’rgan afzal to’g’rimi? Bizning o’rganish obektimiz bizga berigan nuqtalarning deyarli barchasini qanoatlantiruvchi  θ parametrni topish. Buni bajarish uchun funksiya qiymatini hisoblayapmiz yani xatolikning o’rtacha kvadratik funksiyasini. Bizning maqsad shu funksiya qiymatini iloji borija nolga yaqinlashtirish. Xatolikning o’rtacha kavadratik funksiyasi kvadrat funksiyaga keldi( faqatgina bitta parametrga olib kelganimiz uchun), hammamizga malumki kvadrat funksiyada bitta minimum mavjud va bizning vazifa shu minimumni topish. Keling yana grafikda ko’ramiz:

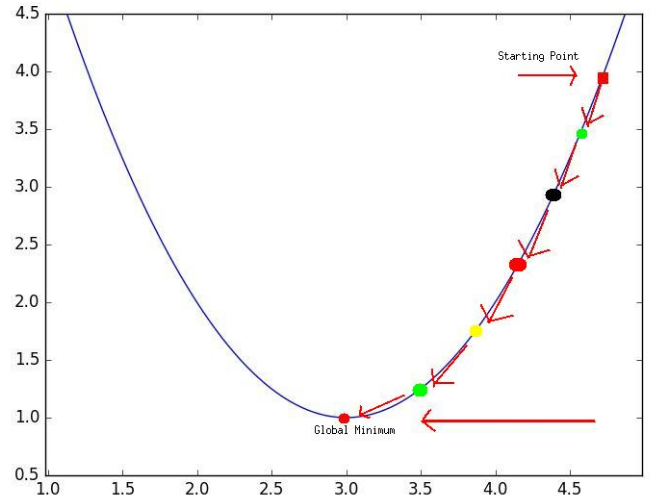
Esingizda bo’lsa yuqorida parameter θ ni tasodifiy tanlab funksiya qiymatini hisoblagan edik. Demak bu tasodifiy tanlangan parameter bilan hisoblangan qiymat minumumdan ancha uzoqda. Endi bu qiymatni qadamma qadam minimumga yaqinlashtirishimiz kerak, lekin buni matemetik yo’l bilan qanday amalga oshiramiz. Bunda bizga funksiya hosilasi yordamga keladi. Agar funksiya bir o’zgaruvchili bo’lsa bunda biz hosila deyishimiz mumkin , ko’p o’zgaruvchili funksiyada esa gradient deymiz(gradient – ko’p o’zgaruvchili funksiya hosilasi). Yani:

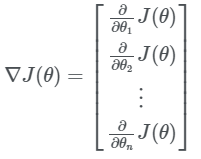
Shu yo’l bilan funksiyamizni minimumga intiltiramiz. Funksiya qiymati minimumga yaqinlashgandagi parametrlar orqali aktivizatsiya funksiyamizni topib olamiz. Demak , o’rganish jarayoni qanday sodir bo’layotgani haqidagi umumiy va chuqurroq tasavurlar paydo bo’ldi degan umiddaman. Yana bir savol qolyapti, kompyuter qanday qilib parametrlarni yangilab boradi? Parametrlarni yangilash: Parametrlarni yangilash quyidagicha amalga oshiriladi:

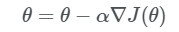
Esda tutushimiz kerakki θ  va ∇J(θ) lar vektorlar. Demak yuqoridagi tenglikni quyidagicha yozsak anqiroq bo’ladi:

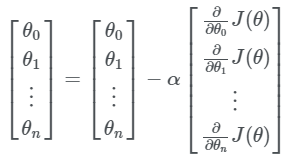
Bu yerda α – o'rganish koifisienti, yani parametrlarning o'zgarish tezligini nazorat qilib turadigan koffisient. O’rganish koffisientini katta olish har doim risky yani havfli bo’lgan, lekin bu koffisientni juda kichik olish ham o’rganish vaqtining juda cho’zilib ketishiga sabab bo’ladi. Keling rasmda ko’ramiz:

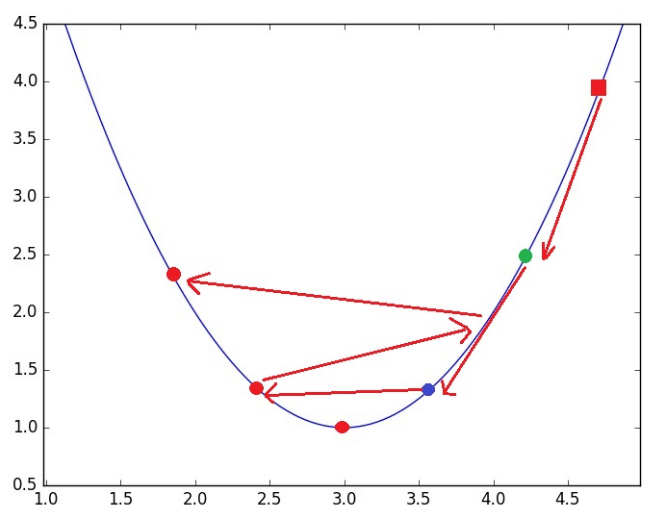
Grafikdan ko’rinib turibdiki o’rganish koffisientini katta olish minimumdan o’tib ketishga yani hech qachon yetmay qolishga sabab bo’lishi mumkin. O’rganish koffisienti haqidagi malumotlarga ega bo’lgandan keyin, gradientni qanday hisoblaymiz degan savolga javob izlasak. Gradient ni hisoblash uchun ko’p o’zgaruvchili funksiyalarning qism hosilalarini hisoblashimiz kerak, bu zanjir qoidasi orqali amalga oshiriladi: Demak natijalar: Og’irliklar uchun: (for weights)

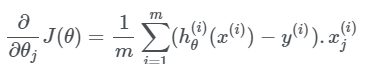
Baislar uchun:

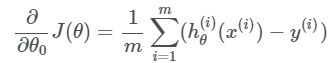
Hammasini umumlashtiradigan bo’lsak quyidagiga ega bo’lamiz:

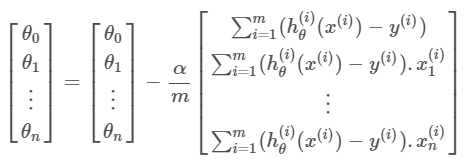
Keling hisoblashlarni amalga oshirib natija qanday o’zgarishini kuzatamiz: θ0=1, θ1=1 bo’lgan hol uchun funksiya qiymati J(θ).

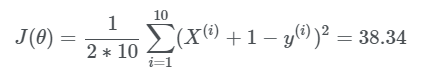
Ko’rinib turibdiki natija juda katta va bu yaxshi natija emas. Gradient tushush orqali parametrlarni yangilaymiz: O’rganish koffisentini α=0.03 deb olamiz:

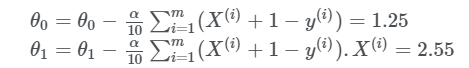
Endi funksiya qiymatini qaytadan hisoblaymiz:

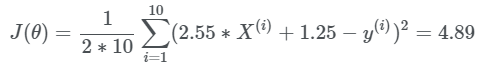
Ko’rib turganingizdek natija anca yaxshilandi yani nolga yaqinlashdi. Keling shu parametrlar bilan aktivizatsiya funksiyamizning grafigini chizamiz:

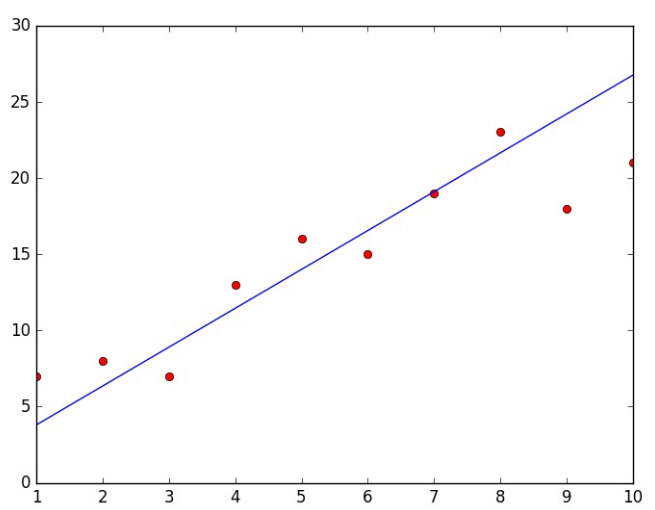
Demak hali ham yanada yaxshilashimiz kerak ekan, yuqorida keltirlgan qadam lar orqali ishni yana takrorlaymiz va parametrlarni yangilab boramiz va 4 qadamdan keyin quyidagi natijaga ega bo’lamiz;

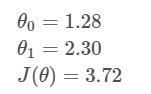
Keling grafikda ham ko’ramiz:

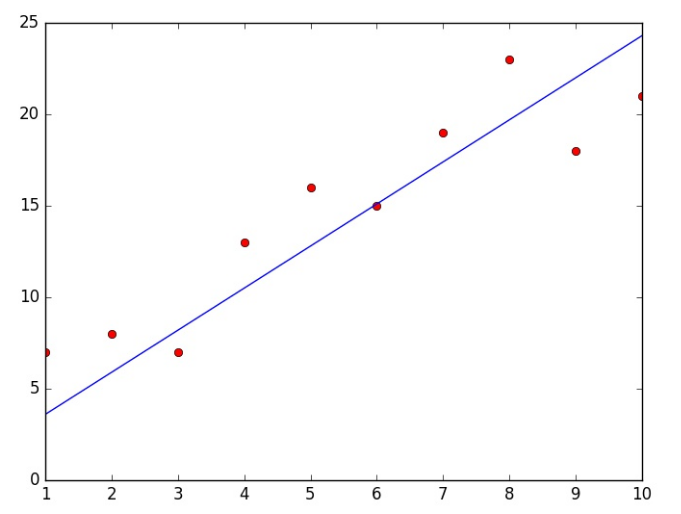
Ko’rib turganingizdek aktivizatsiya funksiyasi grafigi bizning nuqtalarga yaqinlashdi, takrorlashlar orqali funksiya qiymatini yanada minimallashtirishimiz mumkin. Bu eng oddiy va tushunarli algoritm orqali sizga o’rganish jarayoni qanday sodir bo’layotganini tushuntirishga harakat qildim. Umid qilamanki bunga qisman bo’lsa erishdim. Keyingi mavzuda chiziqli regressiyaning 2-qismiga o’tamiz va python dasturlash tili yordamida o’rganganlarimizni tatbiq qilamiz. Hozircha shular, yanada qiziqarli malumotlar bilan ko’rushguncha deb qolaman!