Machine Learning Part4
Machine Learning part 4:«Underfitting and overfitting» muammolari.
ML 4-qismiga keldik. Oldingi darslarimizda chiziqli regressiyani davom ettirishimiz va kod yozishimiz haqida gapirgan edim. Buning uchun sizga python tilini oz muncha tushunishingiz va scikit-learn python based libraryni ham o’rnatishingiz kerak bo’ladi. Buni bajarishni eng sodda yo’li( bu albatta mening shaxsiy fikrim) Anaconda web based envoriment ni o’rnatishingiz deb o’ylayman. Yana bugungi darsimizda MLdagi eng katta muammolardan biri underfitting va overfitting haqida ham gaplashamiz.
Demak boshladik , eng muhimi sizda python va scikit-learn, numpy, pyplot o’rnatilgan bo’lishi kerak.
Bizga kerakli library larni yuklab olamiz:
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
Biz faqat chiziqli regressiya modulidan foydalib qolmay, numpy (vector va matritsalarni ifodalash uchun ), pyplot (grafiklar chizsh uchun) , kabi (python kutubxonalari,)modullardan foydalanamiz. Esingizda bo’lsa o’tgan darsda quyidagi malumotlar bazasidan foydalangan edik:
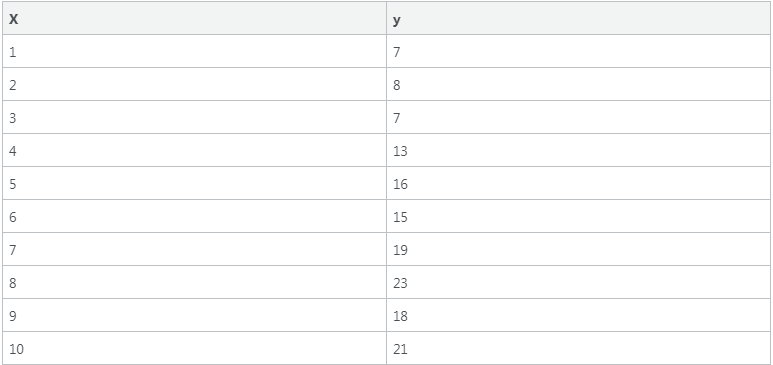
Shundan foydalanib o’rganuvchi malumotlar bazamizni tayyorlab olamiz:
X = np.arange(1, 11).reshape(10, 1)
y = np.array([7, 8, 7, 13, 16, 15, 19, 23, 18, 21]).reshape(10, 1)
Deyarli hamma ML kutubhonalari yuqoridagi formatda bo’lishi kerak yani har bir qator bitta o’rnaniluvchi misol, va har bir ustun bitta atribut yani belgi. Keling malumotlarimizni grafik ko'rinishda tasvirlaymiz:
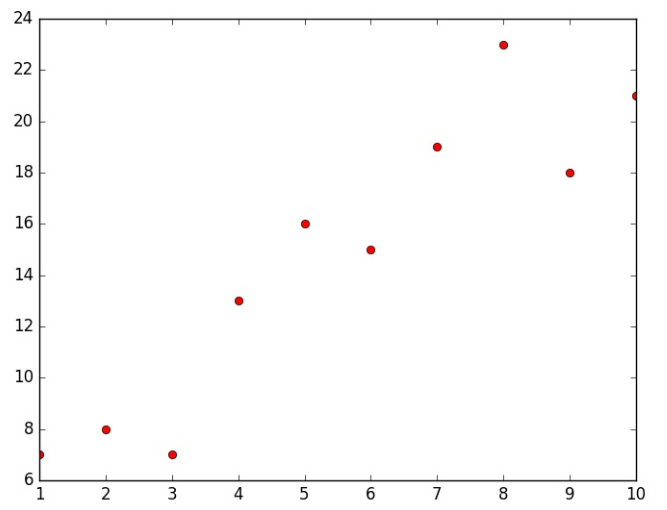Endi, chiziqli regressiya modulimizni ishga tushuramiz:
model = LinearRegression()
fit funksiyasi orqali o’rganish jarayonini yuqoridagi malumotlar bazasida boshlab yuboramiz:
model.fit(X, y)
Bizning malumotlar bazamiz juda kichik va oddiy shunday ekan o’rganish jarayoni juda tez yakunlanadi, va quyida natijalarni ko’rish mumkin:
model.coef_
array([[ 1.77575758]])
model.intercept_
array([ 4.93333333])
coef_- og’irliklar uchun(weights) va intercept_ basilar uchun.
Endi basharoat vektori a ni hisoblaymiz, yuqorida ega bo’lgan o’g’irlik va baislardan foydalangan holda albatta:
a = model.coef_ * X + model.intercept_
Keling hamma vektorlarni bitta grafikda tasvirlaymiz:
axes = plt.gca()
axes.set_ylim([0, 30])
plt.show()
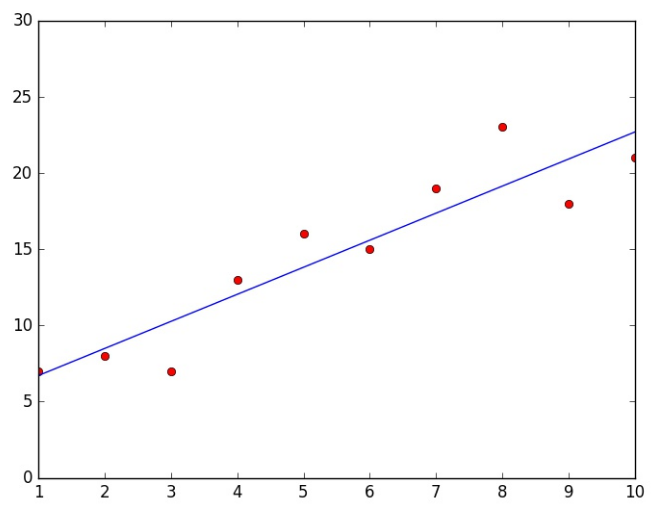
Juda oddiymi? Bir necha qator kod va hammsi bajarilgan! Biz bajargan ish malumotlar bazasini tayyorlash, modelni o’rgatish va natijani vizuallashtirish. Bu albatta scikit-learn kutubxonasining yordami bilan!
Chiziqli regressiya ishini yaxshilash!
Biz erishgan natija yaxshi, lekin yanada yaxshilashga imkon mavjud. Keling modelimizning aniqlik darajasini tekshirib olamiz, buning uchun bizda score() funksiyasi mavjud:
print(model.score(X, y))
0.84988070842366825
Ko’rib turganingizdek biz 85% aniqlik darajasiga erishganmiz , lekin buni yanada yaxshilash yani 90-95% ga olib kelish imkoni mavjud. Qanday qilib ? Atributlar sonini oshirish orqali, esingizda bo’lsa atributlar bu obekt belgilari edi, demak obekt belgilari soni oshishi bilan obektni farqlashdagi aniqlik ham oshadi.
Buning eng sodda yo’li, berilgan atributlar orqali polinomal atributlarni hosil qilish yani, bizda X bor bo’lsa X^2, X^3 kabi atributlarni qo’shish orqali. Keling boshlaymiz:
X = np.c_[X, X**2]
print(X)
array([[ 1, 1],
[ 2, 4],
[ 3, 9],
[ 4, 16],
[ 5, 25],
[ 6, 36],
[ 7, 49],
[ 8, 64],
[ 9, 81],
[ 10, 100]])
Yuqorida aytib o’tgan qadamlarni yana qaytadan bajaramiz;
model.fit(X, y)
x = np.arange(1, 11, 0.1)
x = np.c_[x, x**2]
a = np.dot(x, model.coef_.transpose()) + model.intercept_
Aktivizatsiya funksiyamizning matematik ko’rinishi quyidagicha:
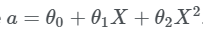X matritsa ozroq murakkab ko’rinishda, shu sababli endilikda dot funksiyasidan foydalanamiz. Yana biz kichkina x o’zgaruvchini ham yaratdik, aktivizatsiya funksiya grafigi tushunarliroq ko’rinishi uchun. Keling grafikda koramiz:
plt.plot(X[:, 0], y, 'ro', x[:, 0], a)
plt.show()
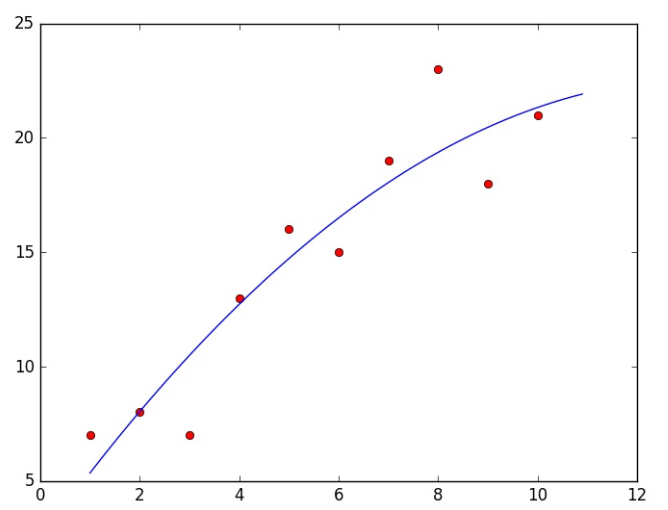Ko’rinib turibdiki natija ancha yaxshilandi. Aniqroq raqmlarda ko’ramiz:
model.score(X, y)
0.87215506914951546
87 % yuqoriroq aniqlik.
Endi o’ylayotgan bo’lishingiz mumkin, demak polinomal atributlarnin ko’paytirib natijani yanada yaxshilashimiz mumkin ekanda deb! Afsuski unday emas! Keling tekshirib ko’ramiz, 9-darajagacha polinomal atributlarni qo’shamiz:
X = np.arange(1, 11)
X = np.c_[X, X**2, X**3, X**4, X**5, X**6, X**7, X**8, X**9]
x = np.arange(1, 11, 0.1)
x = np.c_[x, x**2, x**3, x**4, x**5, x**6, x**7, x**8, x**9]
model.fit(X, y)
a = np.dot(x, model.coef_.transpose()) + model.intercept_
plt.plot(X[:, 0], y, 'ro', x[:, 0], a)
axes = plt.gca()
axes.set_ylim([0, 30])
plt.show()
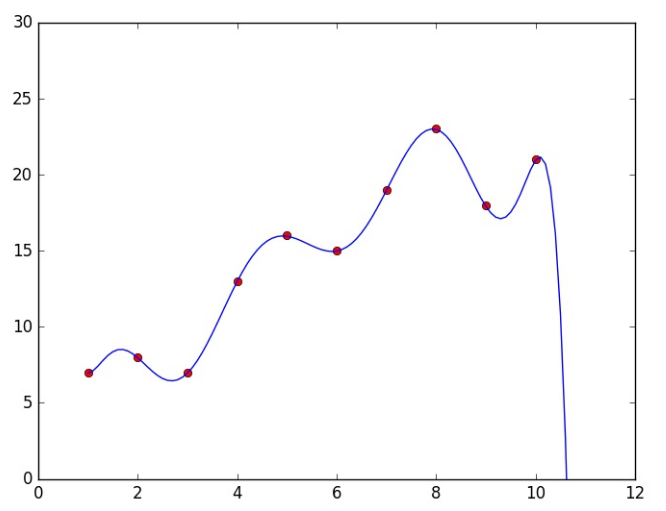Aniqlik darajasini raqamlarda ko’ramiz:
model.score(X, y)
0.99992550472904074
deyarli 100 % aniqlik. Lekin bu model yaxshiligini anglatmaydi!
OVERFITTING & UNDERFITTING muammolari.
Endi tasavur qiling bizda 15ta misoldan iborat malumotlar bazasi bor edi, lekin men sizga ulardan 10 tasinigina ko'rsatgandim. Quyida qolgan 5 tasi:
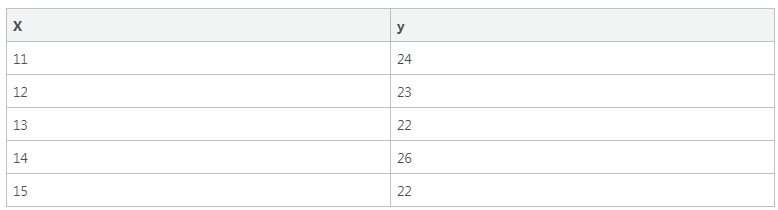Demak to’liq malumotlar bazamiz quyidagicha:
X = np.arange(1, 16)
y = np.append(y, [24, 23, 22, 26, 22])
plt.plot(X, y, 'ro')
plt.show()
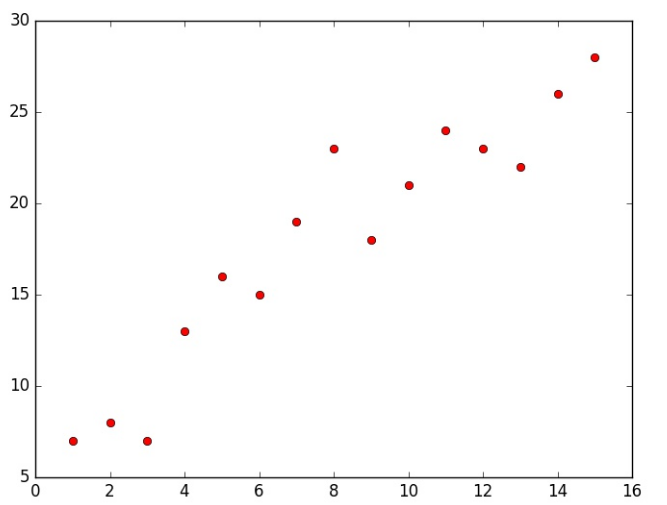
Keling 100% aniqlikka erishga modelimiz bilan bu malumotlar bazasini tekshirib ko’ramiz:
plt.plot(X, y, 'ro', x[:, 0], a)
axes = plt.gca()
axes.set_ylim([0, 30])
plt.show()
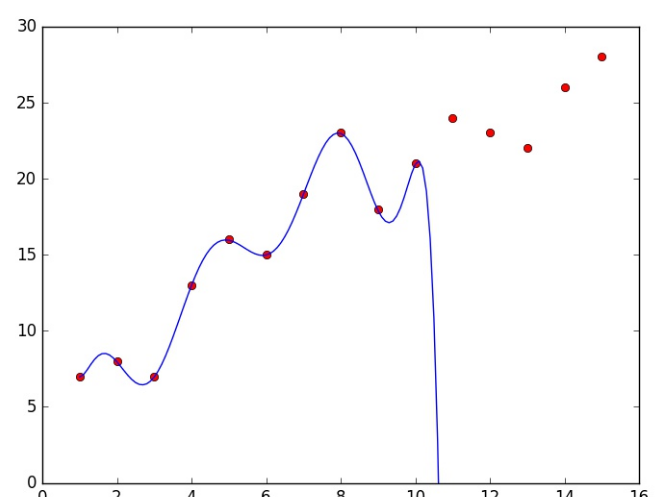
Ko’ryapsizmi? Bizning model yangi malumotlarni umuman tanimadi! Aniqlik darajasini ko’rib o’tirmasak ham natija yomonligini bilishimiz mumkin.
MLda esa model o’rgangan malumotlar bazasi orqali yangi malumotlar bazasini bashorat qilo olishi kerak. Lekin bu model unday qila olmadi. Bu muammo MLda “overfitting” deb yuritiladi. Model malumotlar bazasini o’rganmadi balki yodlab oldi, va yangi malumotlar bilan ishlay olmadi.
Birinchi yaratgan modelimizni eslaysizmi? Bitta atribut bilan unda aniqlik darajasi juda kichik edi, bu muammo MLda “underfitting” deb yuritiladi, yani atributlarning yetishmasligi, belgilar kamligi desak ham bo’ladi.
Yuqoridagi muammolardan biz doima yiroqda bo’lishga harakat qilishimiz kerak. Buning juda ko’p yo’llari o’ylab topilgan, albatta bular haqida ham gaplashamiz.
Bularni hal qilishda birinchi qadam, malumotlar bazasini bo’lish. Yani o’rganiluvchi va test qilinuvchi malumaotlar bazasiga (training and testing datasets). Bu yo’l bilan overfitting problemasini hal qilishimiz mumkin.
Underfitting ga keladigan bo’lsak aniqlik darajasi ham bu muammo qay darajada ekanligini ko’rsatib beradi va yangi atributlar topishga undaydi.
Keling malumotlar bazasini bo’lish orqali yaratgan uchala modelimizni tekshirib ko’ramaiz:
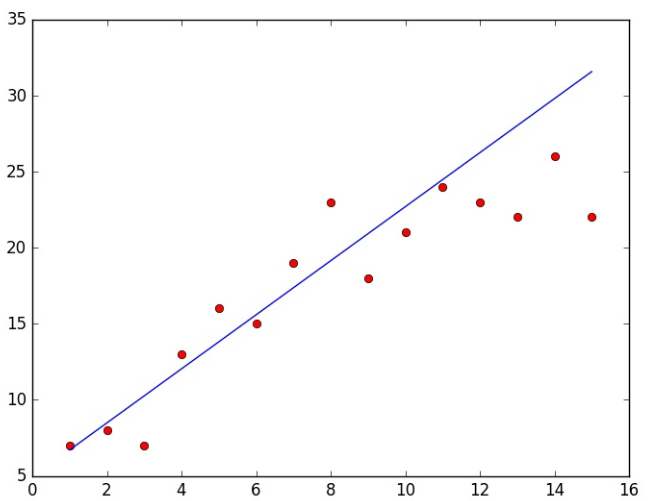
Model 1:
X = np.arange(1, 16).reshape(15, 1)
model.fit(X[:10], y[:10])
model.score(X[10:], y[10:])
-12.653810835629017
a = np.dot(X, model.coef_.transpose()) + model.intercept_
plt.plot(X, y, 'ro', X, a)
plt.show()
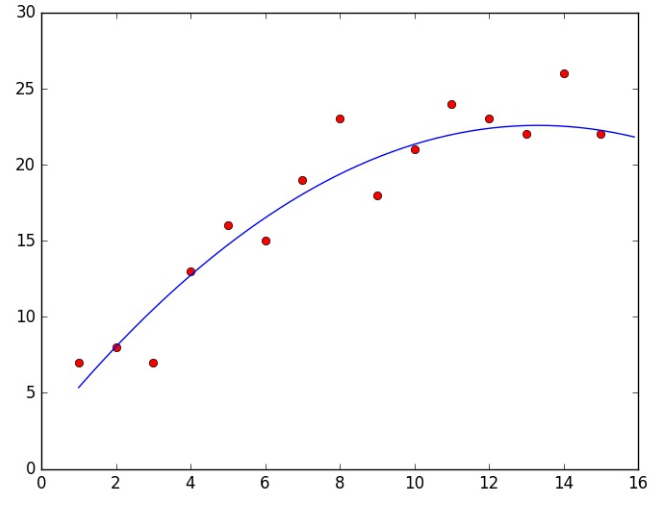
Model 2:
X = np.arange(1, 16).reshape(15, 1)
X = np.c_[X, X**2]
x = np.arange(1, 16, 0.1)
x = np.c_[x, x**2]
model.fit(X[:10], y[:10])
model.score(X[10:], y[10:])
-0.51814820280729812
a = np.dot(x, model.coef_.transpose()) + model.intercept_
plt.plot(X[:, 0], y, 'ro', x[:, 0], a)
axes = plt.gca()
axes.set_ylim([0, 30])
plt.show()
Model 3:
X = np.arange(1, 16).reshape(15, 1)
X = np.c_[X, X**2, X**3, X**4, X**5, X**6, X**7, X**8, X**9]
x = np.arange(1, 16, 0.1)
x = np.c_[x, x**2, x**3, x**4, x**5, x**6, x**7, x**8, x**9]
model.fit(X[:10], y[:10])
model.score(X[10:], y[10:])
-384608869887696.81
a = np.dot(x, model.coef_.transpose()) + model.intercept_
plt.plot(X[:, 0], y, 'ro', x[:, 0], a)
axes = plt.gca()
axes.set_ylim([0, 30])
plt.show()
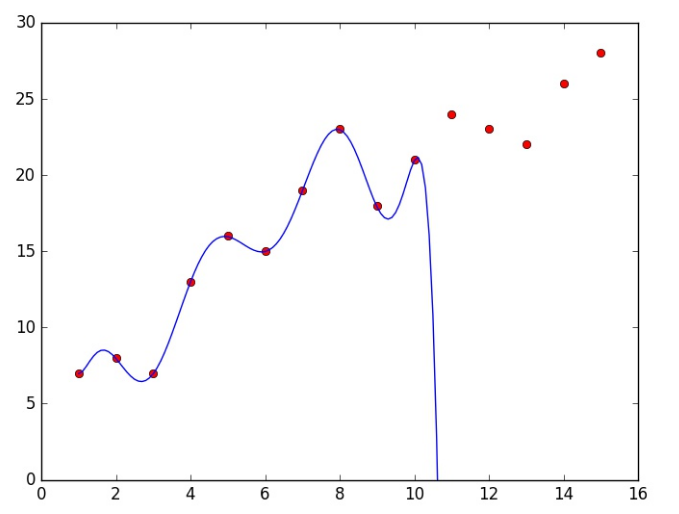
Xulosa shundayki, 2- model eng yaxshisi bo’p qolyapti. Eng muhimi bugungi mavzuda MLda eng ko’p uchraydigan muammolar bilan tanishdik. Malumotlar bazasini 2 ga ajratib o’rganish ham bu muammolarni hal qilishda eng oddiy va foydali usul ekanligini ham bilib oldik. Keyingi mavzularda Mantiqiy regressiya bilan tanishamiz. Ko’rushguncha!